Problem Statement
You are given an n x n integer matrix grid.
Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:
maxLocal[i][j]is equal to the largest value of the3 x 3matrix ingridcentered around rowi + 1and columnj + 1.
In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.
Return the generated matrix.
Examples
Example 1:
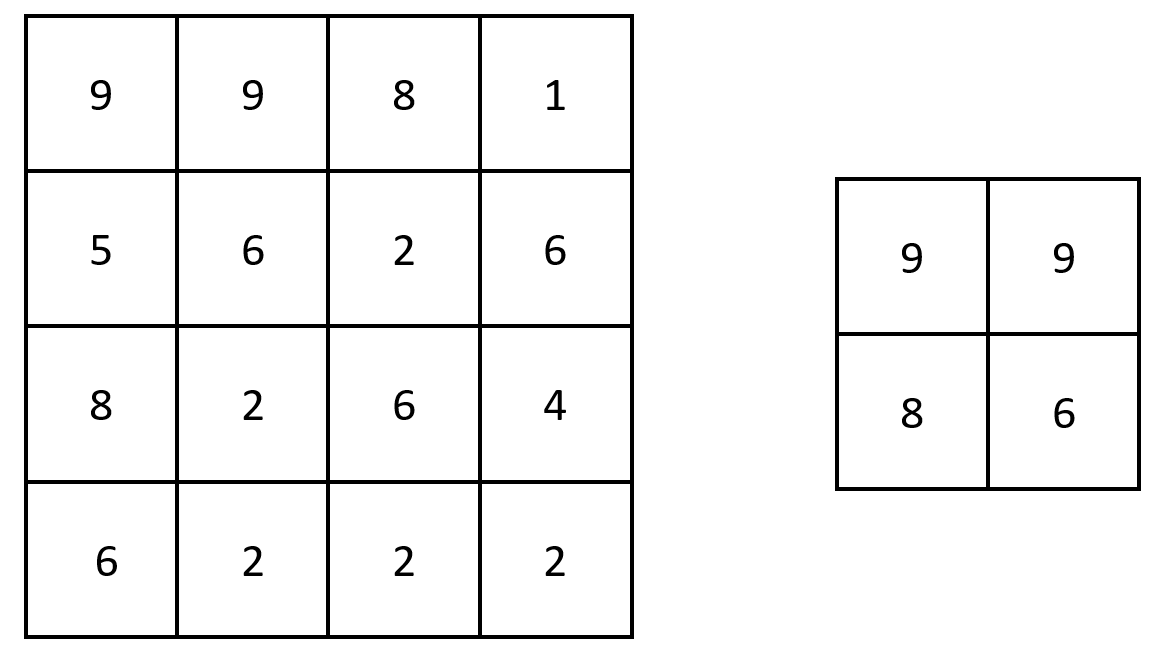
Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
Output: [[9,9],[8,6]]
Explanation: The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
Example 2:
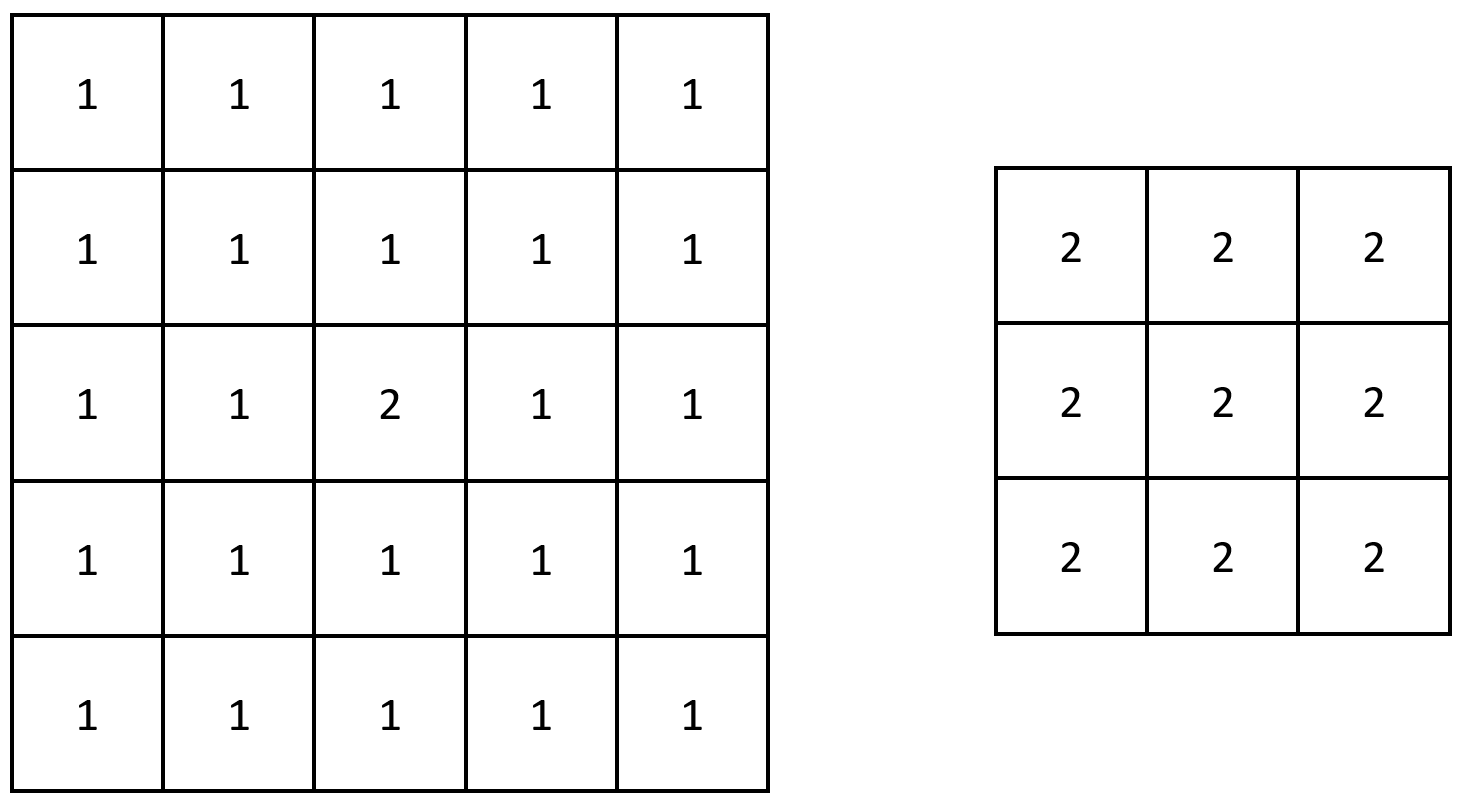
Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
Output: [[2,2,2],[2,2,2],[2,2,2]]
Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
Constraints
n == grid.length == grid[i].length3 <= n <= 1001 <= grid[i][j] <= 100
Intuition
In this question we need to find the max value in a sub-grid of size 3*3, given a grid of size n*n. For every n*n grid the number of 3*3 grids inside it will be (n-2)*(n-2). So for a given grid of size n*n our result grid will always be of size (n-2)*(n-2).
How can we do this? We can loop over each row and column and then loop over each 3*3 sub-grid for ith and jth row and column respectively. Then keep a variable to keep track of the max value in that sub-grid. Append this value to the appropriate index in the result array. This approach is pretty brute force, we can make small tweaks to make it better.
To make the solution better, we can do the following:
iterate till
n-2rather than n. As iterating to the edge will not be useful as on the edges there will be no valid 3*3 sub-grid.Initialize our result grid with zeroes and directly use the result grid index to compare the max.
Lets see the code for this approach.
Code Solution
# TC: O(n^2)
# SC: O(1), if we don't consider res as allocation as we're returning it.
class Solution:
def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:
# initialize n as length of grid
n=len(grid)
# initalize result variable with 0s
# of size (n-2)*(n-2)
res=[[0]*(n-2) for _ in range(n-2)]
# iterate over rows till n-2 rows
for row in range(n-2):
# iterate over columns till n-2 cols
for col in range(n-2):
# check the inner square of 3*3
for inner_row in range(row,row+3):
for inner_col in range(col,col+3):
# put max of current result[row][col] and grid's current index
res[row][col]=max(res[row][col],grid[inner_row][inner_col])
# return the result
return res
Time and Space complexity
Time Complexity:
$$O(n^2)$$
As we're iterating over a grid
Space Complexity:
$$O(1),\ if\ we\ don't\ consider\ result\ array.$$
$$ O(n),\ if\ we\ consider\ result\ array.$$
Conclusion
In this problem we get to learn how to solve an easy grid problem.
Hope that explanation made sense and you found this blog helpful. If you've made it this far, please give it a like and drop a comment.
Happy Coding!🚀
