Problem Statement

You are given an m x n binary matrix grid.

A move consists of choosing any row or column and toggling each value in that row or column (i.e., changing all 0's to 1's, and all 1's to 0's).

Every row of the matrix is interpreted as a binary number, and the score of the matrix is the sum of these numbers.

Return the highest possible score after making any number of moves (including zero moves).

Examples

Example 1:

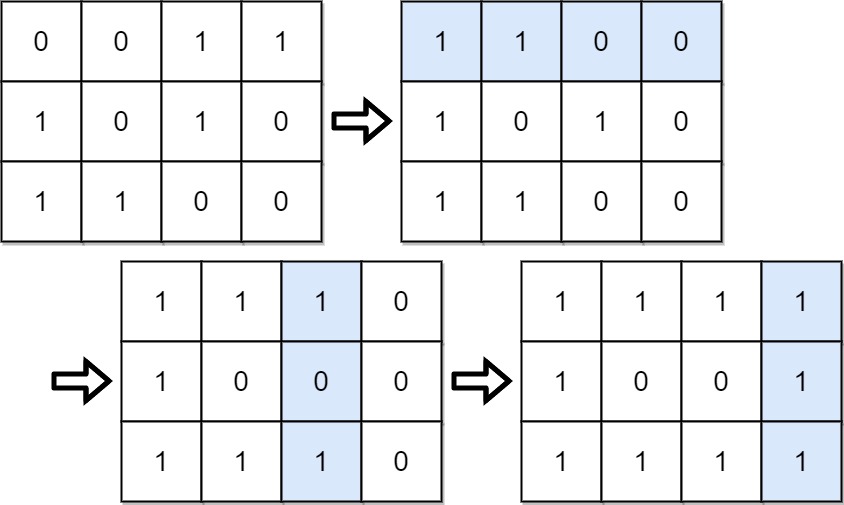
Input: grid = [[0,0,1,1],[1,0,1,0],[1,1,0,0]]
Output: 39
Explanation: 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39

Example 2:

Input: grid = [[0]]
Output: 1

Constraints

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 20

• grid[i][j] is either 0 or 1.

Intuition

So, the task in this problem is quite simple. We need to flip the rows and columns as many times as we want to ensure that the sum of integers formed by the binary representation in a row is maximized.

In order to achieve this, we need to ensure that the Most Significant Bit of each row is maximized. This implies that the leftmost element (or the 0th element of each row) is set to 1. Once we establish this, we can go through the columns starting from the second column. We check whether flipping results in more 1s or 0s. If flipping leads to more 1s, we proceed with the flip; otherwise, we ignore it.

Following this algorithm we can easily maximize the sum of binary representation of each row.

Code Solution

Python Code:

class Solution:
    def matrixScore(self, grid: List[List[int]]) -> int:
        # initialize rows and column size
        rows,cols=len(grid),len(grid[0])
        # make the MSB of each row as 1 if needed
        for row in range(rows):
            # flip MSB if its zero to one
            if grid[row][0]==0:
                self.flipRow(grid,row,cols)
        # iterate from 2nd col
        # check if by flippinf column do we get more 1s, if not don't do anything
        for col in range(1,cols):
            if sum(grid[row][col] for row in range(rows))*2<rows:
                self.flipCol(grid,col,rows)
        # return the sum of numbers formed by bunary representation in a row
        return sum(self.convertBinaryInRow(row) for row in grid)

    # this function flips 0s to 1 and 1s to 0 for a row
    def flipRow(self,grid,row,cols):
        for col in range(cols):
            grid[row][col]=1-grid[row][col]

    # this function flips 0s to 1 and 1s to 0 for a col
    def flipCol(self,grid,col,rows):
        for row in range(rows):
            grid[row][col]=1-grid[row][col]
    # this function forms integer from bunary representation in the row
    def convertBinaryInRow(self,row):
        return int(''.join([str(num) for num in row]),2)

Time and Space complexity

Time Complexity:

$$O(n^2)$$

As we're iterating over a grid.

Space Complexity:

$$O(1)$$

As we don't allocate any extra space.

Conclusion

In this problem we just have to figure out how binary numbers work. If we maximize the most significant bit, we're already in a good position. After that we just have to see if flipping each column would do us any good or not.

Hope that explanation made sense and you found this blog helpful. If you've made it this far, please give it a like and drop a comment.

Happy Coding!🚀