Recursion, a programming concept where a function calls itself, might sound like a mind-bender at first. But fear not! This powerful technique is surprisingly intuitive and can be a valuable tool in your Pythonic arsenal. In this blog, we'll embark on a recursive journey, exploring its core principles, implementation in Python, and visualization with recursive call-stack diagrams.

Understanding Recursion: A Function Calling Itself

Imagine a set of Russian nesting dolls. To open the biggest doll, you need to open the one inside it, and to open that one, you need an even smaller doll within it, and so on. Recursion works similarly. A function breaks down a larger problem into a smaller version of itself, and this process continues until a base case, a simple condition that can be solved directly, is reached.

Visualizing the Recursive Flow: Call-stack Diagrams

Let's use a classic example – calculating the factorial of a number (denoted by n!). The factorial is the product of all positive integers less than or equal to n. For instance, 5! (factorial of 5) is 5 x 4 x 3 x 2 x 1 = 120.

Here's a recursive function in Python to calculate factorial:

def factorial(n):
  # base case
  if n == 0:
    return 1
# recursive case
  else:
    return n * factorial(n-1)

his function checks if the input n is 0. If it is, the base case is reached, and we simply return 1 (the factorial of 0). Otherwise, the function multiplies n by the factorial of n-1, essentially calling itself with a smaller value.

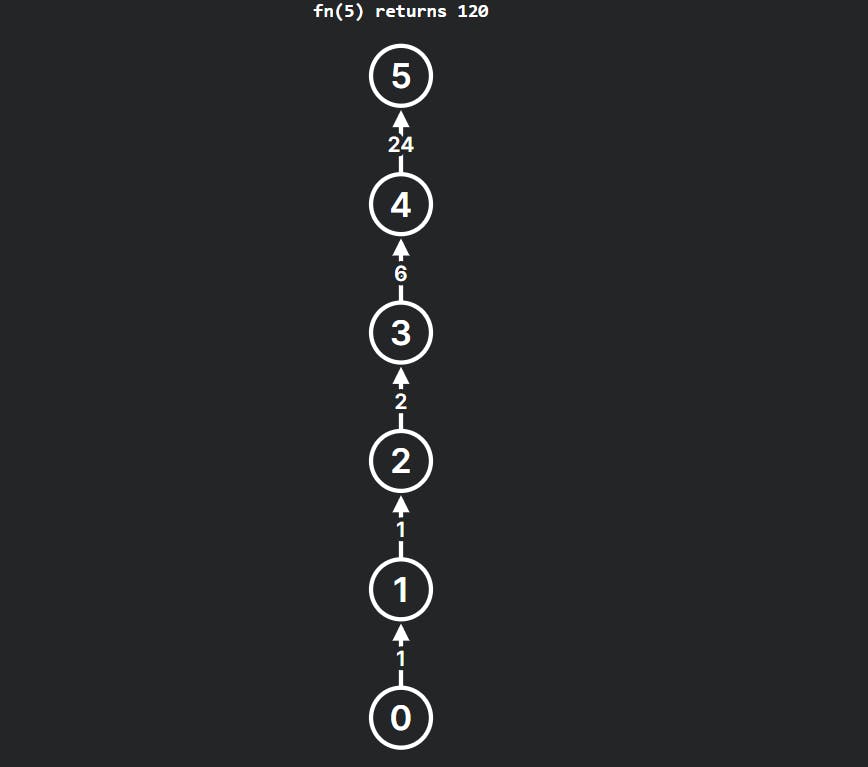
This diagram shows nested rectangles representing function calls, with the calling function positioned above the called function. Arrows indicate the flow of execution. As you can see, factorial(5) calls factorial(4), which in turn calls factorial(3), and so on, until the base case (factorial(0)) is reached. The results then bubble back up, calculating the final factorial of 5 which is 120.

How to use recursion

We can use recursion by doing the following:

• Identify actual problem: in the above example actual problem is to find the factorial of n .

• Identify sub-problem: in the above example in order to get factorial(n) we will have to find factorial(n-1)*factorial(n-2).....*factorial(1) . The factorial(n-1),factorial(n-2), etc are the sub-problems.

• Trust that the base function works: we trust that our factorial function works for all sub-problems and will give correct answer.

Link actual and sub-problem: in the example above our actual and sub-problem are related like this:

$$f(n)=f(n-1)*f(n-2)$$

• Identify base condition: the base case is very important in a recursive function as it tells the program when to stop calling the recursive function.

Important parts of a recursive function

There are two important parts of a recursive function:

1. Base Case: This is the simplest scenario that does not require further recursion. It's the terminating condition for the recursive calls. Without a base case, the function would call itself indefinitely, leading to a stack overflow error.

   In the above example of factorial the lines:

    # basecase  
    if n == 0:
        return 1
   

   is the base case.

2. Recursive Case: This is the part where the function actually calls itself. However, the input to the recursive call must be a smaller version of the original problem. This ensures that the function eventually reaches the base case and terminates.

   In the above example of factorial the lines:

    # recursive case
      else:
        return n * factorial(n-1)
   

   is the recursive case

In essence, a recursive function breaks down a larger problem into a smaller version of itself (the recursive case) until it reaches a simple enough problem to solve directly (the base case).

More Examples of Recursive Functions

Recursion can be a powerful tool for various problems:

• Fibonacci sequence: This sequence is where each number is the sum of the two preceding numbers. A recursive function can easily calculate the nth Fibonacci number.

• Tree traversals: When working with tree data structures, recursion is a natural fit for traversing the tree nodes in different orders (preorder, inorder, postorder).

• Maze solving: Imagine a robot navigating a maze. Recursion can be used to explore different paths until the exit is found.

The Key to Successful Recursion: The Base Case!

The cornerstone of writing successful recursive functions is ensuring a well-defined base case. Without a base case, the function calls will keep happening infinitely, leading to