In this blog, let's explore how we can tackle the 1137. N-th Tribonacci Number problem using Python and Golang.

Problem Statement

The Tribonacci sequence T_n is defined as follows:

T₀ = 0, T₁ = 1, T₂ = 1, and T_n+3 = T_n + T_n+1 + T_n+2 for n >= 0.

Given n, return the value of T_n.

Examples

Example 1:

Input: n = 4
Output: 4
Explanation:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

Example 2:

Input: n = 25
Output: 1389537

Constraints

• 0 <= n <= 37

• The answer is guaranteed to fit within a 32-bit integer, ie. answer <= 2^31 - 1.

Intuition

The tribonacci is a spin on the classic Fibonacci sequence that can be solved using recursion. In the recursion blog we understood how to use recursion. Lets understand how we can solve this problem using the following steps:

• Identify actual problem: find Tribonacci(n)

• Identify sub-problem: in order to find tribonacci(n) we will have to find tribonacci(n-1), tribonacci(n-2).....tribonacci(1) . So, tribonacci(n-1), tribonacci(n-2), etc will be the sub-problems.

• Trust that the base function works: we trust that the function tribonacci works for all sub-problems and will give correct answer.

• Link actual and sub-problem: as it is already specified in the problem statement, actual and sub-problems are linked like this:

$$trib(n)=trib(n-1)+trib(n-2)+trib(n-3)$$

Identify base condition: Since we can't find tribonacci of -1 as per constraints, we can say that:

        # base condition
        if n==0:
            return 0
        elif n<=2:
            return 1

This will make sure our recursion does not go beyond tribnacci(0).

Solution

Code in python

class Solution:
    def tribonacci(self, n: int) -> int:
        # base condition
        if n==0:
            return 0
        elif n<=2:
            return 1
        # recursive case
        return self.tribonacci(n-1)+self.tribonacci(n-2)+self.tribonacci(n-3)

Code in Go

func tribonacci(n int) int {
    # base condition
    if n==0{
        return 0
    }else if n<=2{
        return 1
    }
    # recursive case
    return tribonacci(n-1)+tribonacci(n-2)+tribonacci(n-3)
}

Note: this code when run on leetcode will give Time Limit Exceeded(TLE).

We will enhance this code in Dynamic Programming series to reduce its Time and Space complexity

Time and Space complexity

Time Complexity:

$${O(3^n)}$$

this is because for each recursive function call we make three other recursive calls.

Space complexity:

If you notice here we're not utilizing any data-structure, but since we're using recursion, for every recursive call the compiler will allocate space in heap for the recursive call-stack. Hence space complexity will be:

$$O(n)$$

Recursive Call Stack

Here's the recursive call stack for tribonacci(5):

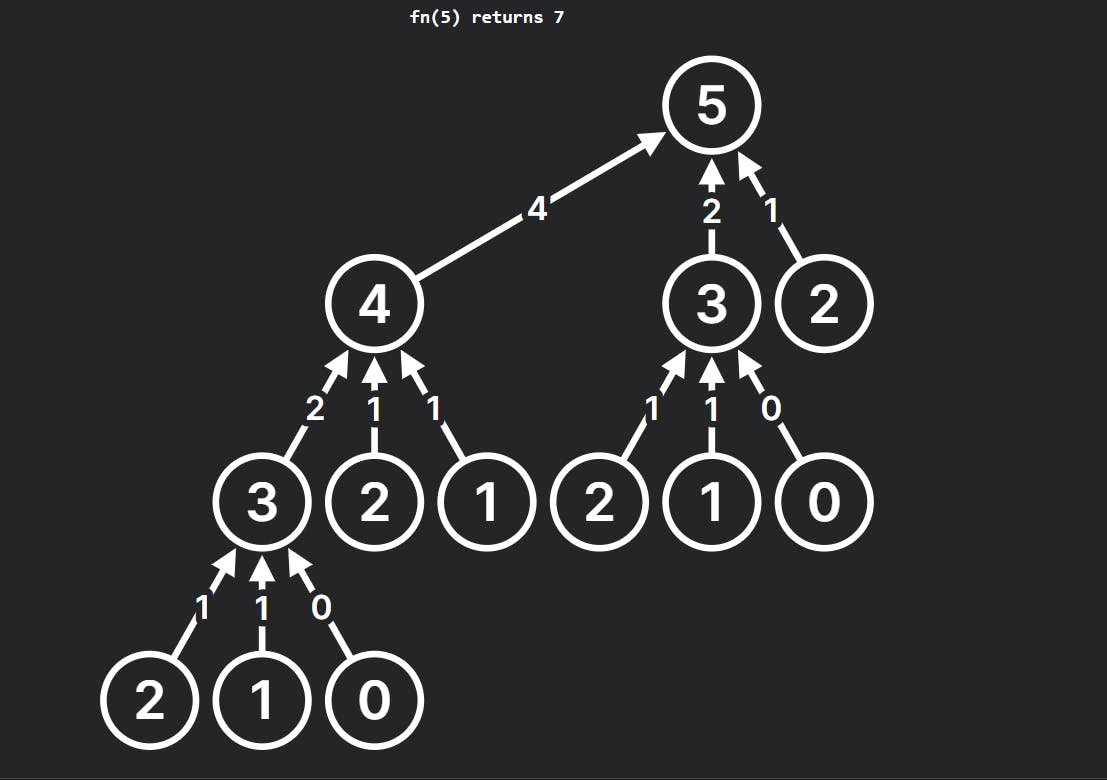
I hope you've picked up how recursion can tackle the tribonacci problem.

If you found this post helpful, give it a like and drop a comment.

Happy Coding! 🚀